Excelは文理問わず私たちの日常生活に欠かせない優れた表計算ソフトだが、その演算結果に誤差が含まれていることをご存じだろうか。大手電機メーカーで計算機ソフトウェアの開発に20年間従事した記者が、誤差の原因と回避法を解説する。
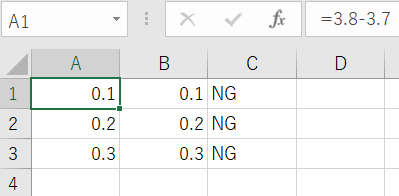
Excelのセルに次のように入力してみる。
| A列 | B列 | C列 | |
| 1行 | 3.8-3.7 | 0.1 | =IF(A1=B1, “OK”, “NG”) |
| 2行 | 305.2-305 | 0.2 | =IF(A2=B2, “OK”, “NG”) |
| 3行 | 115.5-115.2 | 0.3 | =IF(A3=B3, “OK”, “NG”) |
A列の計算結果は、B列の0.1、0.2、0.3という簡単な数だ。ところがC列で関数を使用して計算結果の成否を判別すると、以下のようにA列とB列の値は異なるものと判定される。
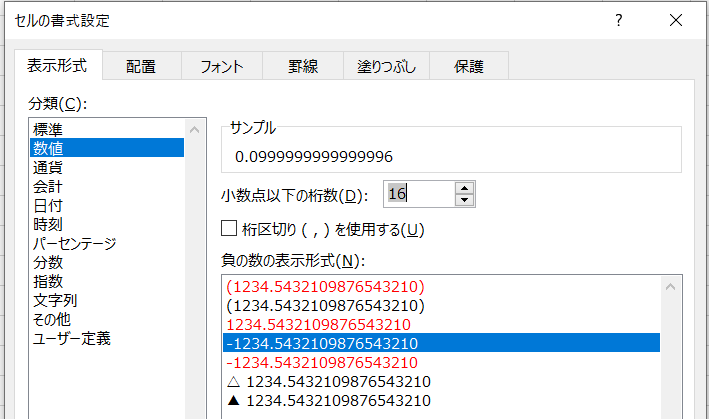
なぜこのようになるのか。A列の表示設定を変えて、小数点以下16桁まで表示させると明らかになる。
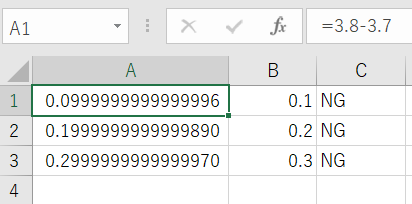
上記のように、セルの書式設定で小数点以下の桁数を16桁に変更すると、以下のように表示される。
A列の計算結果には、16桁表示で見えるようになる微小な計算の誤差が含まれていたのだ。
このようになる原因は二つある。一つは真の値が無限桁であったとしてもコンピュータでは有限桁しか扱えないことだ。無限桁とは、10を3で割った答え（3.3333……）のように、終わりなく桁が続くこと。無限桁に対して、桁がどこかで終わることを有限桁という。もう一つの原因は、コンピュータでは2進数を用いていることだ。2進数は0と1のみで表現する数値。整数を表すときに2，4，8，……と2の倍数の組合せで表す。小数もそれと同じで、1/2，1/4，1/8，……の組合せで表していく。その結果、10進法では切りのいい小数でも、2進数では無限桁の小数になってしまうことが起こりえる。コンピュータでは無限桁を保持することはできない。ExcelはIEEE 754という浮動小数点演算＊の規格に従うように設計されていて、例えば0.1なら2.8×10-17以下は切り捨てられる。
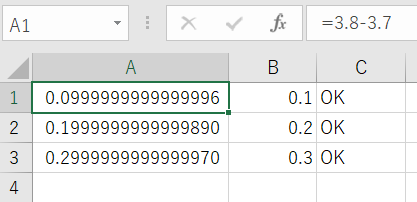
誤差が現れるのは小数の演算であり、その結果をピンポイントで判定すると大きな問題になる。そうならないためには、あらかじめ誤差が生じることを見込んで判定するようにすれば良い。上記の例なら、C列に例えば以下のように入力する。これは相対誤差として10-13を見込んだものだ。
=IF(ABS(A1-B1)<(10^-13)*ABS(B1), “OK”, “NG”)
ABS(B1)が真値の絶対値、ABS(A1-B1)が差分の絶対値で、前者で後者を割ったものが相対誤差になる。ABS(B1)が０や微小な数値でも計算できるように、このように入力する。
Excelのように便利な道具であっても限界はある。無条件に過信して痛い目に合う前に、あらかじめ弱点を知っておいて賢く使えるようにしたいものだ。
＊浮動小数点演算 コンピュータの数値演算方式のひとつで浮動小数点の形で計算すること。浮動小数点とは、数字を仮数、基数、指数の要素に分けて表現すること。基数は10進法なら10、2進法なら2。
（冒頭の写真はイメージ）